
© Merkurtransit.de 2016 - 2019
|
| Zur Startseite |
Planetentransits und die SonnenparallaxeAls Parallaxe bezeichnet man in der Astronomie die scheinbare Verschiebung der Position eines Himmelskörpers vor dem Hintergrund der Fixsterne, wenn man ihn von 2 verschiedenen Standorten aus beobachtet. Je näher ein Objekt der Erde ist, umso größer ist seine Parallaxe und umso geringer ist der Abstand, den 2 Beobachter haben müssen, um die Parallaxe zu messen. So reichen einige hundert Kilometer Distanz aus, um die Parallaxe und damit auch die Entfernung des Mondes zu bestimmen, für die Nachbarplaneten Venus und Mars benötigt man bereits mehrere 1000 Kilometer, selbst wenn Sie wie Mars im Juli 20018 und Venus im Juni 2012 der Erde sehr nahe kommen. Im Prinzip handelt es sich bei der Parallaxenmessung um eine trigonometrische Peilung. 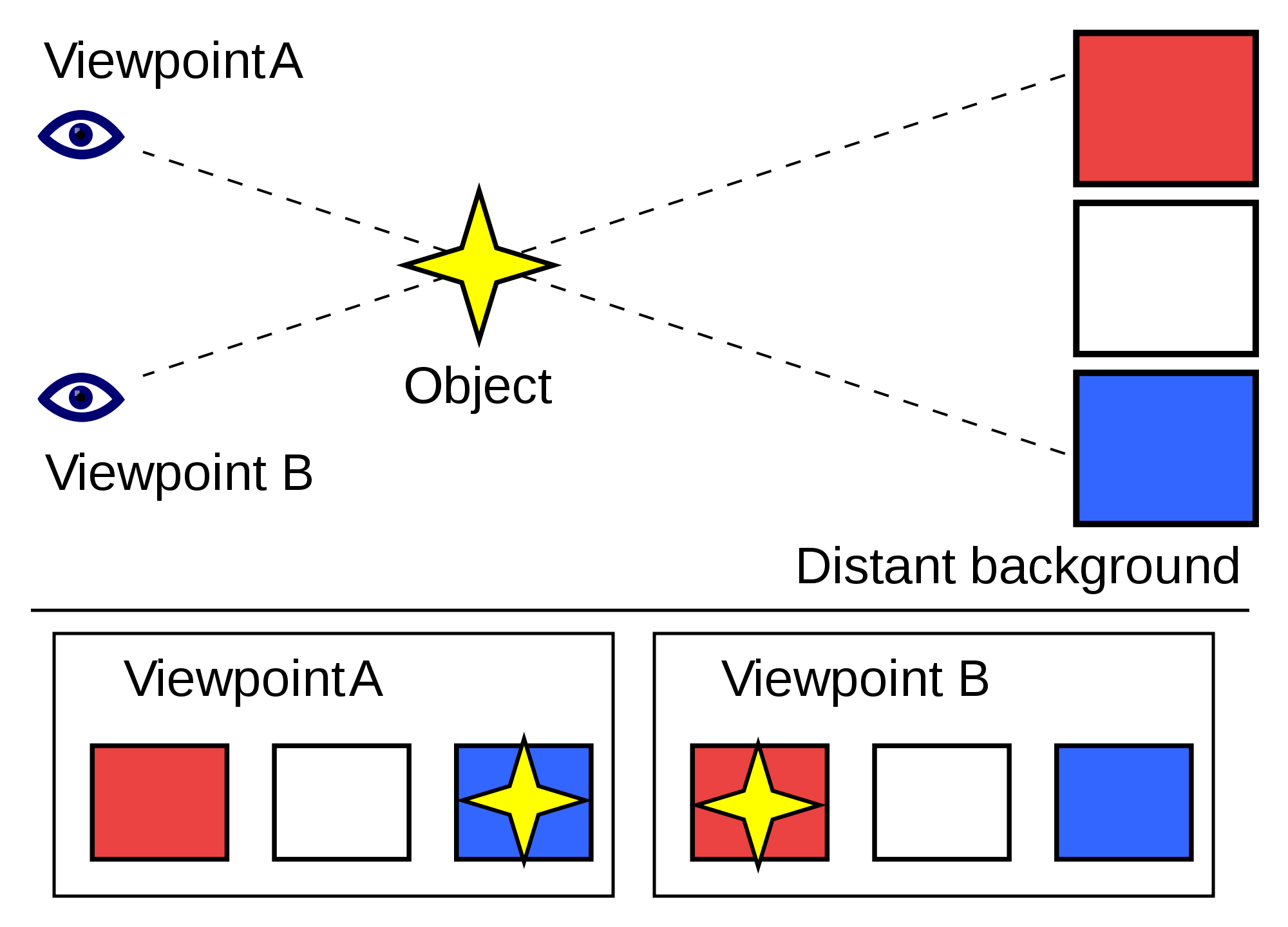
Das Prinzip der Parallaxe. (© Booyabazooka. Diese Abbildung ist lizensiert unter einer Creative Commons License.)
Durch die Arbeiten Johannes Keplers kannte man ab 1627 die relativen Abstände der Planeten untereinander und von der Sonne. Wenn man nur eine Entfernung absolut bestimmen konnte, so waren damit auch alle anderen absoluten Abstände bekannt. Die exakte Vermessung des Sonnensystems war daher in der Zeit nach Kepler die große Aufgabe der Astronomie. Einer der ersten, die sich daran versuchten, war Jeremiah Horrocks. Während des Venustransits 1639 maß er den scheinbaren Durchmesser unseres Nachbarplaneten zu 72 Bogensekunden. Mit der gewagten Annahme, dass die Venus genau so groß sei wie die Erde, kam er auf einen Abstand Erde - Sonne von etwa 95 Millionen Kilometern. In Wirklichkeit ist die Venus etwas kleiner als die Erde und auch ihr scheinbarer Durchmesser bei einem Transit ist geringer. Doch im Vergleich zu der seit der griechischen Antike verwendeten Angabe (ca. 7,5 Millionen km) kam Horrocks mit seinen Überlegungen dem tatsächlichen Wert der Astronomischen Einheit (AE), wie die Entfernung Sonne - Erde jetzt bezeichnet wurde, bereits wesentlich näher. 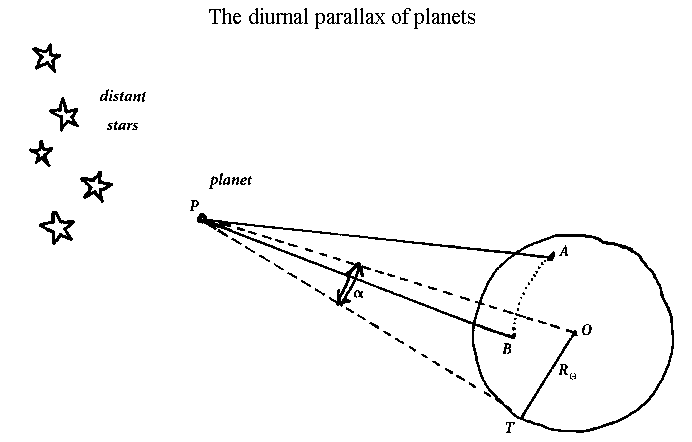
Bestimmung der Mars-Parallaxe nach der Methode von Cassini. (Quelle: EAEE)
Da man sich von der Transit-Methode genauere Ergebnisse versprach, trat die Mars-Methode nach 1672 weitgehend in den Hintergrund. Erst im 19. Jahrhundert wurde sie durch die deutlich besseren Geräte und die zwischenzeitliche Lösung des Längenproblems wieder interessant. Die besten Ergebnisse erzielte man im Jahr 1877, als Mars erneut der Erde sehr nah kam. Die Sonnenparallaxe wurde zu 8.78 Bogensekunden berechnet, was nur noch etwa 1/100 Bogensekunde vom heute anerkannten Wert (8.794 Bogensekunden) abwich (Maunder & Moore 2000, S. 74). Einen noch etwas genaueren Wert erreichte man 1931, als sich der 1898 entdeckte Asteroid Eros der Erde bis auf 26 Millionen Kilometer näherte (Weaver 1943)*. Damit war die Parallaxen-Methode ausgereizt. Die heutigen hochpräzisen Werte für die AE (Genauigkeit +/- 6m) wurden erst ab den 1960er-Jahren durch die Messung der Laufzeit von Radarechos von der Venus gewonnen. * Als Eros der Erde im Januar/Februar 2012 erneut sehr nahe kam, wurde durch Amateurastronomen kurzfristig ein internationales Projekt initiiert, um die historischen Parallaxen-Messungen zu wiederholen (Blog dazu). Im historischen Kontext ist es durchaus verständlich, dass man sich der Venus zuwandte. Niemand konnte wissen, wann es deutlich bessere Geräte geben, wann das Längenproblem gelöst sein würde. Und es war nicht irgendwer, der die Transit-Methode vorschlug, sondern der größte Astronom seiner Zeit - Edmund Halley. Am 7. November 1677 beobachtete der damals erst 21jährige Wissenschaftler auf St. Helena einen Merkurtransit mit bis dahin unerreichter Genauigkeit. Halley kam danach zu dem Schluss, dass ein solcher Planetendurchgang von weit auseinander liegenden Orten auf der Erde beobachtet zur Bestimmung der AE verwendet werden könnte. Besser als Merkur sollte sich allerdings die Venus eignen, kommt sie doch der Erde bei einem Transit wesentlich näher. In dem Wissen, dass er den nächsten Venusdurchgang im Jahr 1761 mit Sicherheit nicht mehr erleben würde, veröffentlichte er im Jahr 1716 seine berühmt gewordene Publikation, in der groß angelegte Expeditionen zur Transit-Beobachtung vorgeschlagen wurde. Zugleich erläuterte er das Prinzip seiner Methode. Halleys Methode ist recht elegant. An Instrumenten werden lediglich ein Teleskop und eine Pendeluhr benötigt. Letztere muss nicht die Ortszeit anzeigen, sie dient lediglich dazu, den Zeitraum zu bestimmen, der zwischen dem 2. und dem 3. Kontakt vergeht. Beobachter, die an weit auseinander liegenden Orten der Erde stationiert sind, werden unterschiedliche Zeitspannen messen. Je mehr Zeit zwischen den Kontakten vergeht desto länger ist die Strecke, welche Venus vor der Sonne zurücklegt. Da die Winkelgeschwindigkeit* der Venus in Unterer Konjunktion auf Grund der Keplerschen Gesetze bekannt ist, lässt sich nun für jeden Beobachtungsort die genaue Lage des Pfades der Venus vor der Sonnenscheibe bestimmen. Aus den geringen Lageunterschieden zwischen den einzelnen Pfaden, welche stets weniger als eine Bogenminute betragen, und der Länge der Basislinie zwischen den Beobachtungsorten auf der Erde errechnet man die Parallaxe der Venus und die der Sonne. Um die Basislinie auf der Erde zu berechnen, benötigt man natürlich die Positionen der Beobachter. Größere Fehler in der Angabe des Längengrades wirken sich auf das Ergebnis der Parallaxen-Bestimmung aus. * Die beobachtete Winkelgeschwindigkeit der Venus kann allerdings geringer oder größer sein. Dies liegt an der Eigenrotation der Erde, welche den Beobachter je nach Standort entweder in oder gegen die Bewegungsrichtung der Venus befördert. Dieser Faktor ist bei der Parallaxen-Berechnung zu berücksichtigen und einer der Gründe, warum diese mathematisch nicht ganz einfach ist. 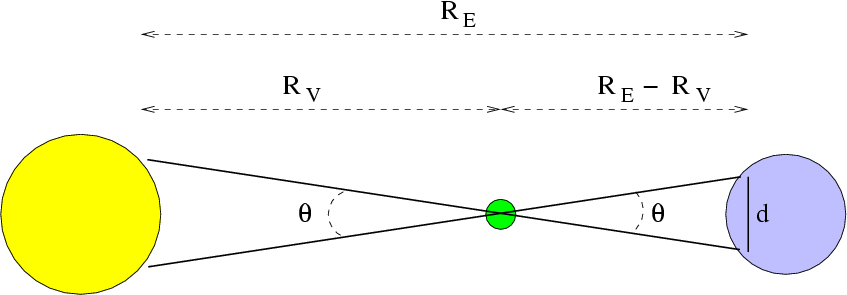
Das Grundprinzip der Transit-Methode (© Michael Richmond. Diese Abbildung ist lizensiert unter einer Creative Commons License)
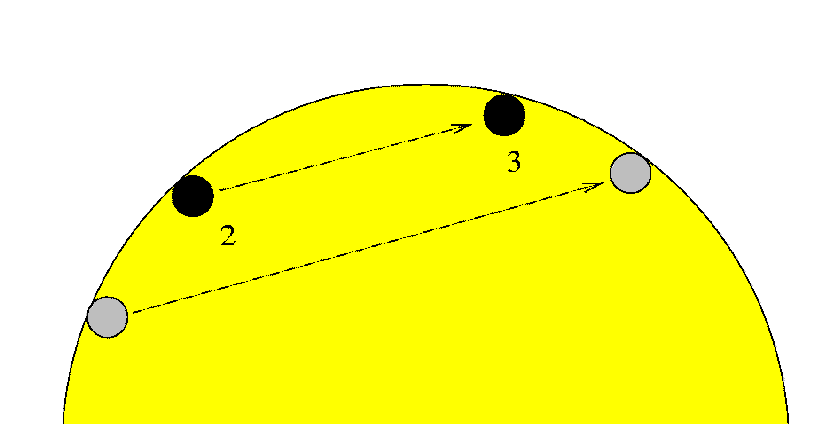
Unterschiedliche Lage des Pfads der Venus vor der Sonne von weit entfernten Orten auf der Erde beobachtet (© Michael Richmond. Diese Abbildung ist lizensiert unter einer Creative Commons License)
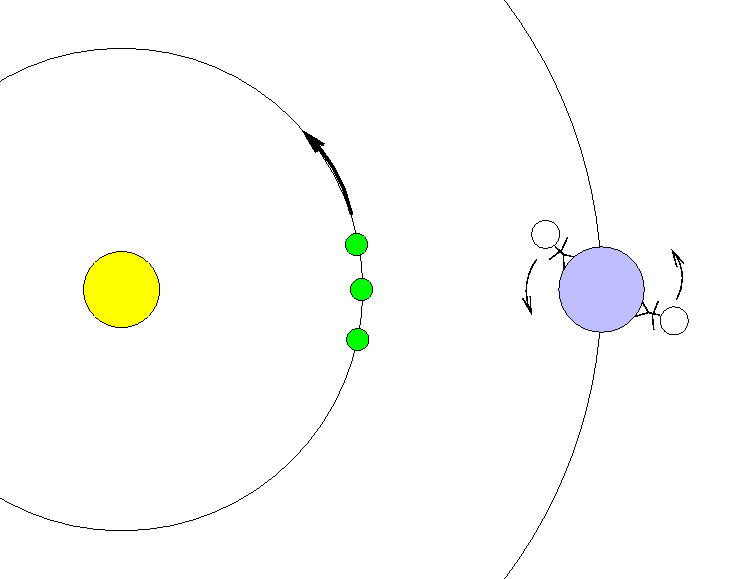
Je nach Standort auf der Erde wirkt sich die Erdrotation unterschiedlich auf die beobachtete Winkelgeschwindigkeit der Venus aus (© Michael Richmond. Diese Abbildung ist lizensiert unter einer Creative Commons License)
Im Jahr 1723 kam es zu einer Begegnung Halleys mit dem französischen Astronomen Joseph-Nicolas Delisle. Delisle, der kurz zuvor (09.11.1723) selber einen Merkurtransit beobachtet hatte, erkannte die Schwäche von Halleys Methode: Da sowohl Eintritt als auch Austritt der Venus aus der Sonnenscheibe gemessen werden mussten, konnte eine Expedition scheitern, wenn sich auch nur bei einem der Kontakte in den entscheidenden Sekunden Wolken vor die Sonne schoben. Zum anderen kamen von vorneherein nur Beobachtungsorte in Frage, an denen der Transit in seinem ganzen Verlauf sichtbar war. Delisle entwickelte daher eine eigene Methode, bei der es im Unterschied zu Halleys Ansatz genügte, den absoluten Zeitpunkt eines der beiden inneren Kontakte zu bestimmen. Aus deren zeitlicher Differenz zwischen unterschiedlichen Orten auf der Erde ließ sich dann wiederum die parallaktische Verschiebung der Venus berechnen. Der Vorteil dieses Ansatzes war, dass auch Beobachtungsorte in Frage kamen, an denen die Sonne während des Transits auf- und unterging, womit sich die Anzahl der erfolgreichen Expeditionen erhöhen würde. Andererseits war es aber zwingend erforderlich, die geografische Länge mit weitaus höherer Präzision zu ermitteln, als es für Halleys Methode erforderlich war. Deshalb mussten die Expeditionen oft lange vor und/oder nach dem Transit am Expeditionsziel bleiben, um mit Hilfe von Finsternissen, Stern- bzw. Planetenbedeckungen durch den Mond, Verfinsterungen der Jupitermonde oder aber Monddistanzen den Längengrad möglichst präzise zu bestimmen. Mit den viel besseren Instrumenten des 20. Jh. erwies sich die Parallaxenmessung bei den Merkurtransits 1970 und 1973 als durchführbar (Protitch-Benishek 1983). Heute ist dies auch mit amateurastronomischen Mitteln möglich; ein entsprechendes Projekt wurde daher anlässlich des Merkurdurcgangs am 09.05.2016 geplant. Bei den Venustransit-Expeditionen 1761 und 1769 kamen sowohl Halleys als auch Delisles Methode zur Anwendung. Doch die Ergebnisse waren ernüchternd, das Phänomen des Schwarzen Tropfens verhinderte eine ausreichend genaue Bestimmung der Kontaktzeiten. Wie wir erst seit dem Venustransit 2004 mit Sicherheit wissen, scheiterte das großartige Unterfangen somit letztlich an der Unzulänglichkeit der verfügbaren Optiken. Doch kann man überhaupt von einem Scheitern sprechen? Nach dem Transit von 1769 kam die Stunde der Mathematiker, welche die verfügbaren Daten aufbereiteten. Jérôme Lalande gab den Wert der Sonnenparallaxe im Jahr 1771 mit 8,59 Bogensekunden an, Alexander Guy Pingré kam auf 8,80 Bogensekunden. Damit lag er, ohne dass es jemand ahnen konnte, fast genau beim heutigen Wert (8.794 Bogensekunden). Die Diskrepanzen in den Berechnungen dieser beiden und anderer waren freilich nicht zu übersehen. Johann Encke bereitete die vorliegenden Daten daher in den 1820er-Jahren noch einmal auf und berechnete die Sonnenparallaxe zu 8.5776 Bogensekunden. Für etwa 30 Jahre war dies nun der in der Literatur allgemein anerkannte Wert, bevor erneute Zweifel aufkamen. Diese waren der Grund für die Renaissance der Mars-Methode seit den 1850er-Jahren. Die größten Hoffnungen setzte man aber auf den bevorstehenden Venustransit 1874, für den erstmals fotografische Methoden zur Verfügung standen. Doch erneut machte der Schwarze Tropfen den Wissenschaftlern das Leben schwer. Man erwartete sich daher vom Venustransit 1882 keine großen Verbesserungen der Genauigkeit mehr. Simon Newcomb nahm sich des Datenmaterials aus beiden Transits an und veröffentlichte im Jahr 1890 eine Wert von 8.79 Bogensekunden für die Sonnen-Parallaxe, womit er dem heutigen Wert auf 0,04 Bogensekunden nahe kam. Die im Jahr 1877 gemessenen Mars-Parallaxen hatten 8.78 Bogensekunden ergeben. Letztlich war allen Widrigkeiten zum Trotz die Transit-Methode von Erfolg gekrönt. Doch dieser Erfolg stellte sich erst zu einer Zeit ein, als wesentlich unaufwendigere Verfahren (neben der Mars-Methode vor allem Parallaxen-Bestimmungen an Hauptgürtel-Asteroiden wie Flora) bereits zu ebenso guten Ergebnissen führten. 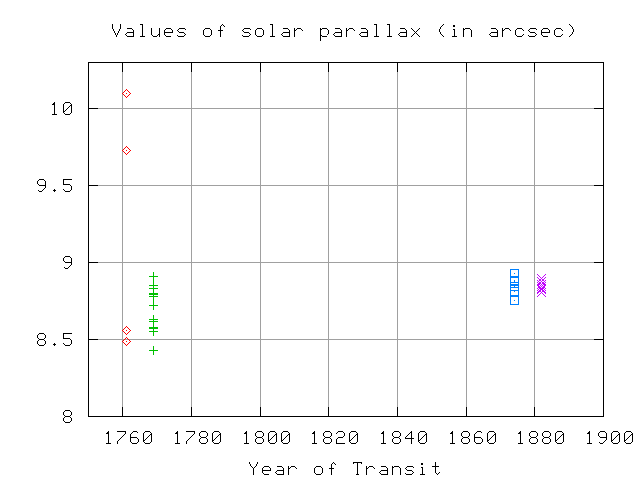
Werte für die Sonnenparallaxe auf Grund der Beobachtungen bei den Venustransits im 18. und 19. Jh.
(© Michael Richmond. Diese Abbildung ist lizensiert unter einer Creative Commons License) Quellen & Links:
Astro!nfo: Berechnung der Venusdistanz aus der Transitdauer Udo Backhaus: Die Entfernung der Sonne (PDF) EAEE: Measuring distances by parallax method Jürgen Giesen: Halley und die Sonnenparallaxe Jan Hattenbach: Asteroid (433) Eros: so nah wie seit 37 Jahren nicht mehr Michael Maunder & Patrick Moore (1999): Transit - When planets cross the sun. 164 S., Springer-Verlag, London - Berlin - Heidelberg. Protitch-Benishek, V. (1983): Transits of Mercury - Results of Belgrade observations in 1970 and 1973. Astronomische Nachrichten 304 (6), 313-315. Michael Richmond: Transits of Venus William Sheehan & John Westfall (2004): The Transits of Venus. 407 S., Prometheus Books, Amherst, New York. H. F. Weaver (1943): The Solar Parallax. Astronomical Society of the Pacific Leaflets 4, 144-151. |